O-Levels Math: How to Complete the Square Easily?
- Mr Ausome
- Dec 26, 2017
- 2 min read

Completing the square of a quadratic equation is a very useful technique that is used for solving quadratic equations(E-Math), finding the turning point of a quadratic graph (E-Math) and finding the center of a circles equation (A-Math). However, students often forget the method and ask me frequently during our math tuition classes.
In this article, I will try to make the process of completing the square as simple and digestible as possible, but I will not further elaborate on the background reasoning behind it.
Fundamental Step of Completing Square
The key thing to completing the square is to remember this:
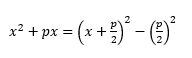
Formulas can be difficult to appreciate without the help of numbers.
Observe the pattern in the following examples of completing the square to understand the above formula:
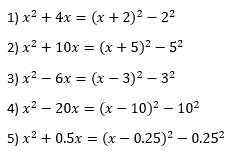
To remember a formula, you have to practice!
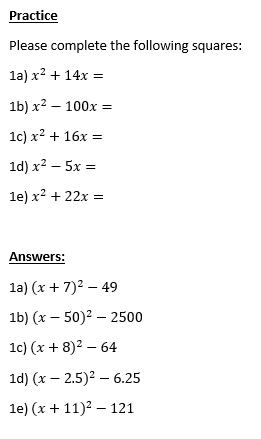
Completing the Square for a Typical Quadratic Equation
After learning the core step in completing the square, we will have to apply it on a typical quadratic equation which has 3 terms. We complete the square the same way as the above section and we simply carry the x-independent term along.
Observe the pattern in the following examples of completing the square:
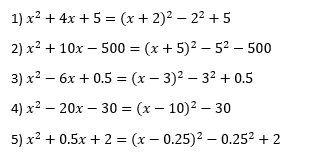
*Note that only the crucial step has been shown above. Please further simplify the equation by yourself.
Time to test your understanding through practice!
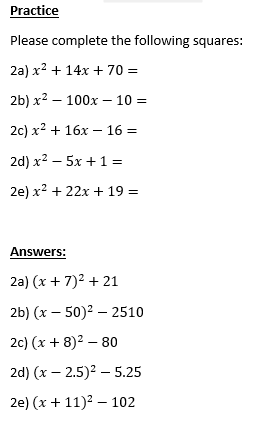
Completing the Square of more Complex Quadratic Equations
In the previous parts, all the equations start with x^2. So how to we complete the square for equations where the x^2 has a different coefficient?
For example, how do we complete the square of


Done!
Now you have understood the art of completing the square! It is actually a very simple concept and yet students forget it again and again. Just make sure you remember the core formula above and you practice enough!
"Don't practice until you get it right, practice until you can't get it wrong!"
~ Unknown
To get professional help (Math tuition) on secondary school mathematics in Singapore, click here.
Mr Ausome















Comments